SOLUTION 7 The domain of f is all xvaluesNow determine a sign chart for the first derivative, f' Then f'(x) = 1 3 (1/3) x 1/31 = 1 x2/3 = 0 when x 2/3 1 = 0 Thus, x 2/3 = 1 so that and x = 1 or x = 1 In addition, note that f' is NOT DEFINED at x=0 To avoid using a calculator, it is convenient to use numbers like x= 8, 1/8, 1/8, and 8 as "test points" to construct theIf f(x)=∫ (5x^87x^6)/(x^212x^7 )^2 dx,(x≥0), and f(0)=0, then the value of f(1) is(a) 1/2(b) 1/4(c) 1/2(d) 1/4To buy complete Course please Visit–httpExample 2 f(x) = x n where n = 1, 2, 3 d In this example we answer the question "What is x n ?" Once we know the dx answer we can use it to, for example, find the derivative of f(x) = x4 by replacing n by 4 At this point in our studies, we only know one tool for finding derivatives – the difference quotient

Answered 4 1 32 F T 2 I 1 O 33 Bartleby
F(x)=2(1/7)^x
F(x)=2(1/7)^x-Aug 21, 15 · So, f (x) = − 10 x 7 5x5 C Now, f (1) = − 10 1 7 5(1) C = 0 gets us C = 43 5 and f (x) = − 10 x 7 5x5 43 5 Answer linkSuppose you are given the two functions f (x) = 2x 3 and g(x) = –x 2 5Composition means that you can plug g(x) into f (x)This is written as "(f o g)(x)", which is pronounced as "fcomposeg of x"And "( f o g)(x)" means "f (g(x))"That is, you plug something in for x, then you plug that value into g, simplify, and then plug the result into f




7 Identify Any Holes In The Graph Of F X X 7 7x Chegg Com
R > 0 then the function de–ned by f (x) = X1 n=0 c n (x a) n = c 0 c 1 (x a) c 2 (x a) 2 is di⁄erentiable (hence) continuous on (a R;aR) and 1 f0 (x) = c 1 2c 2 (x a)3c 3 (x a) 2 In other words, the series can be di⁄erentiated term by term 2 R f (x)dx = C c 0 (x a)c 1 (x a)2 2 c 2 (x a)3 3 In other words, theThe range of f(x)=2^x would be the y values This would include all values that would be the output for the y value An example of this would be if you used 2 as x then the function would read f(x)=2^2 The y would equal 4 which would be included in the range of this function To find the domain and range of the inverse you would follow the(x 2)2 After cancellation, we get lim x!2 (x 1)(x 2) (x 2)2 = lim x!2 (x 1) (x 2) Now this is a rational function where the numerator approaches 1 as x!2 and the denominator approaches 0 as x!2 Therefore lim x!2 (x 1) (x 2) does not exist We can analyze this limit a little further, by checking out the left and right hand limits at 2 As
In this math video lesson I review how to graph the exponential equation y=2^x by making a table The table helps when graphing these types of equations #eDon't get too concerned about "x", it is just there to show us where the input goes and what happens to itInverse f (x)=1/7 x2/7 \square!
Part II f x is continuous on ab, , F x is an antiderivative off x (ie F xfxdx ) then b a f xdx Fb F a Variants of Part I ux a d f tdt u x f ux dx b vx d f tdt v x f vx dx () () ux vx ux vx d ftdt u x f v x fX 0 1 2 3 4 5 6 7 8 9 Enter each answer as a whole number (like4, 0, or 253) or DNE for undefined orClick here👆to get an answer to your question ️ If the function fR→ R defined by f(x) = 4^x4^x2 , then show that f(1 x) = 1 f(x) , and hence deduce the value of f (14) 2f (12) f (34)




Let F X X2 3x 9 Compute The Following A Chegg Com




Calculus For Business Economics And The Social And Life Scienc Brief Edition 11th Edition Hoffmann S By Hazard333 Issuu
Becomes an output of 16 In fact we can write f(4) = 16 The "x" is Just a PlaceHolder!Transcribed image text 6 y = f(x) 5 5 1 4 3 اليفة 2 1 !Contact Pro Premium Expert Support »




If The Function F X X 3 3 1 7 X 2 3 A 2 9 X 1 Has A Posit
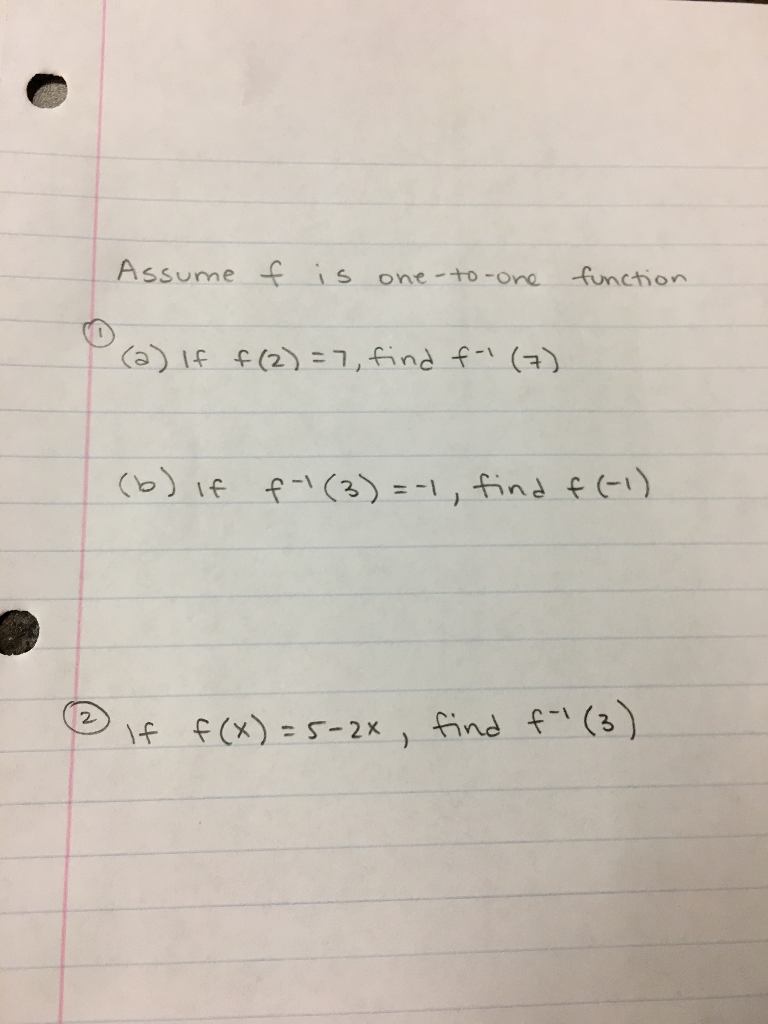



Assume F One To One Function If F 2 Find F 1 Chegg Com
22 Evaluate square root of 72 √72 72 23 Evaluate square root of (2)^4 √(−2)4 ( 2) 4 24Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Start with the given function Replace f (x) with 'y' Switch x and y Subtract 2 from both sides Divide both sides by 3 Rearrange the equation So the inverse function is which is a function




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12




Answered Questions 15 16 The Table Below Bartleby
Simple and best practice solution for f(x)=x^315x^210x96 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework= 2x 3 x 2 2 The domain of (f g)(x) consists of all xvalues that are in the domain of both f and g In this example, f and g both have domain consisting of all real numbers, therefore (f g)(x) also has domain consisting of all real numbers The Difference of Two FunctionsIf a horizontal line intersects the graph of f(x) in more than one point, then f(x) is not onetoone The reason f(x) would not be onetoone is that the graph would contain two points that have the same second coordinate – for example, (2,3) and (4,3) That would mean that f(2) and f(4) both equal 3, and onetoone




Find The Remainder When Polynomial 4x 4 3x 3 2x 2 X 7 Is Divided By X 1 X 1 2x 1




If F Mathbb R Setminus 0 1 To Mathbb R Satisfies F X 2f Left Frac 1 X Right 3f Left Frac X X 1 Right X Then 8f 4 Mathematics Stack Exchange
Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect squareThis preview shows page 25 28 out of 32 pages Hence x 3 is a point of discontinuity 2 Consider the function f (x) = (x 2x2 x2, x 6 = 2 1, x = 2 Here f (2) = 1 is defined and lim x → 2 f (x) = lim x → 2 x 2x2 x2 = 3 exists But lim x → 2 f (x) = 3 6 = f (2) = 1 Therefore f is discontinuous at 2 3 Consider the function f (x) = (2 x 2, x 6 = 0 1, x = 0 25Jan 28, · Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?
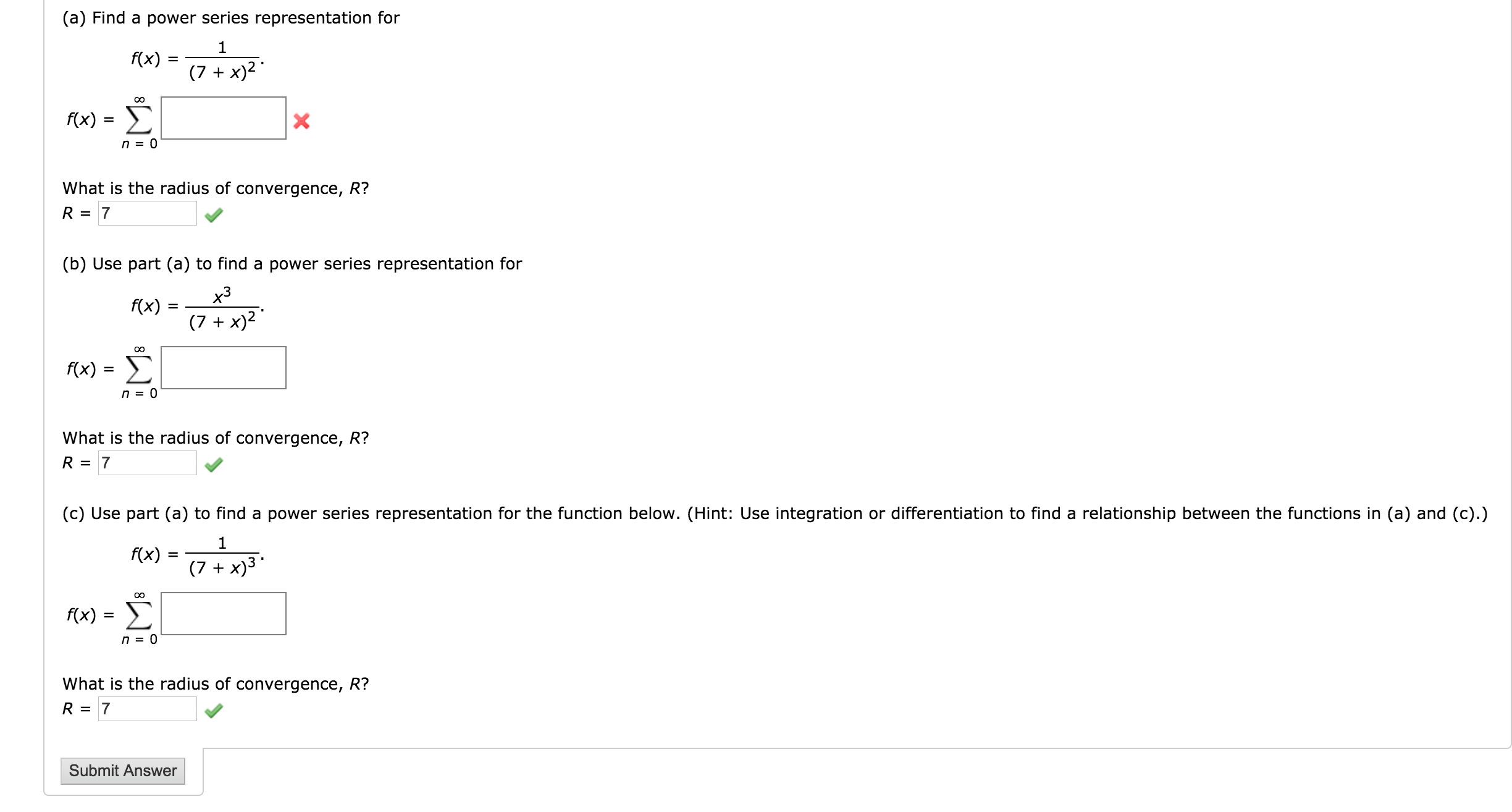



Solved Find A Power Series Representation For F X 1 7 Chegg Com




Find The Domain And Range Of F X 7x 2 4x 1 Brainly In
Now that we can find the inverse of a function, we will explore the graphs of functions and their inverses Let us return to the quadratic function f (x) = x 2 f (x) = x 2 restricted to the domain 0, ∞), 0, ∞), on which this function is onetoone, and graph it as in Figure 7Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website!It is given that f(x) = sin x and g(x) = x^2 For h(x) = fog(x) h(x) = f(g(x)) = f(x^2) = sin (x^2) The derivative h'(x) can be determined by using the chain rule




1 Given The Functions F X X 1 And G X 3 X Chegg Com




Part 1 1 Point Use Differentiation And Or Chegg Com
Domain of f (x) = x/ (x^21) WolframAlpha Have a question about using WolframAlpha?Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of yF(x) = x 2 shows us that function "f" takes "x" and squares it Example with f(x) = x 2 an input of 4 ;




Wirtschaftsmathematik Pdf Free Download
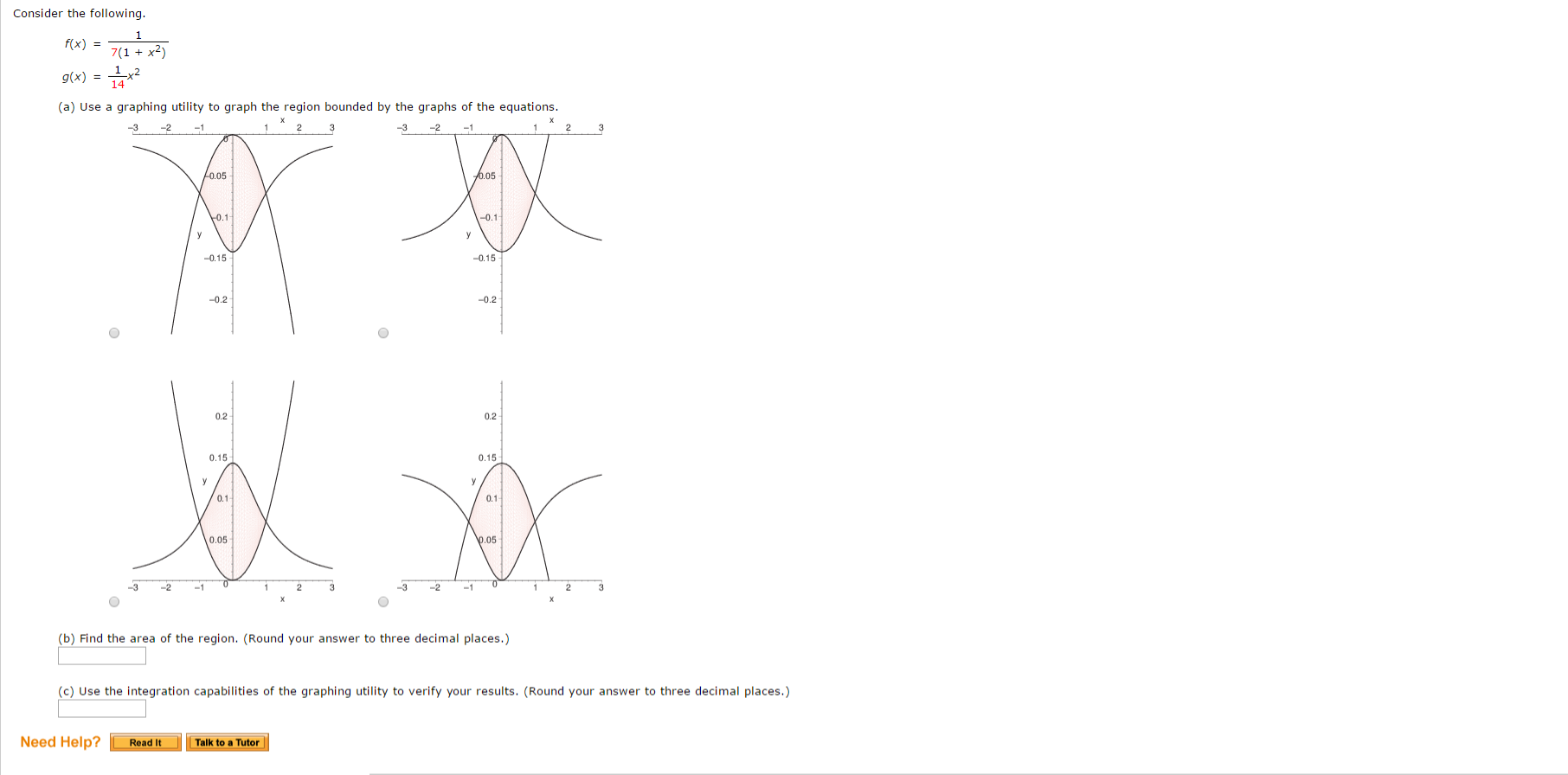



Solved Consider The Following F X 1 7 1 X 2 G X Chegg Com
Nov 30, 19 · Ex 131, 31 If the function f(x) satisfies lim┬(x → 1) (𝑓(𝑥) − 2)/(𝑥2 − 1) = π , evaluate lim┬(x→1) f(x) Given lim┬(x→1) (𝑓(𝑥) − 2Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context This looks much worse than2 for twice differentiable functions, show ∇2f(x) 0 3 show that f is obtained from simple convex functions by operations that preserve convexity • nonnegative weighted sum • composition with affine function • pointwise maximum and supremum • composition • minimization




If F X 2x 3 13x 2 17x 12 Find F 2




Answered 4 1 32 F T 2 I 1 O 33 Bartleby
Steps for Solving Linear Equation F ^ { 1 } ( x ) = \frac { x 6 } { 7 } F 1 ( x) = 7 x 6 Multiply both sides of the equation by 7 Multiply both sides of the equation by 7 7F^ {1}x=x6 7 F 1 x = x 6 Calculate F to the power of 1 and get F Calculate F to the power of 1 and get FThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5 The same notion may also be used to show how a function affects particular values Example f(4) = 4 2 5 =21, f(10) = (10) 2 5 = 105 or alternatively f x → x 2 5 The phrase "y is a function of x" means that the value of y depends upon the value ofFunction of X The function FX(x) is also called the distributionfunction of X 162 Properties of a CumulativeDistribution Function The valuesFX(X)of the distributionfunction of a discrete random variable X satisfythe conditions 1 F(∞)= 0 and F(∞)=1;
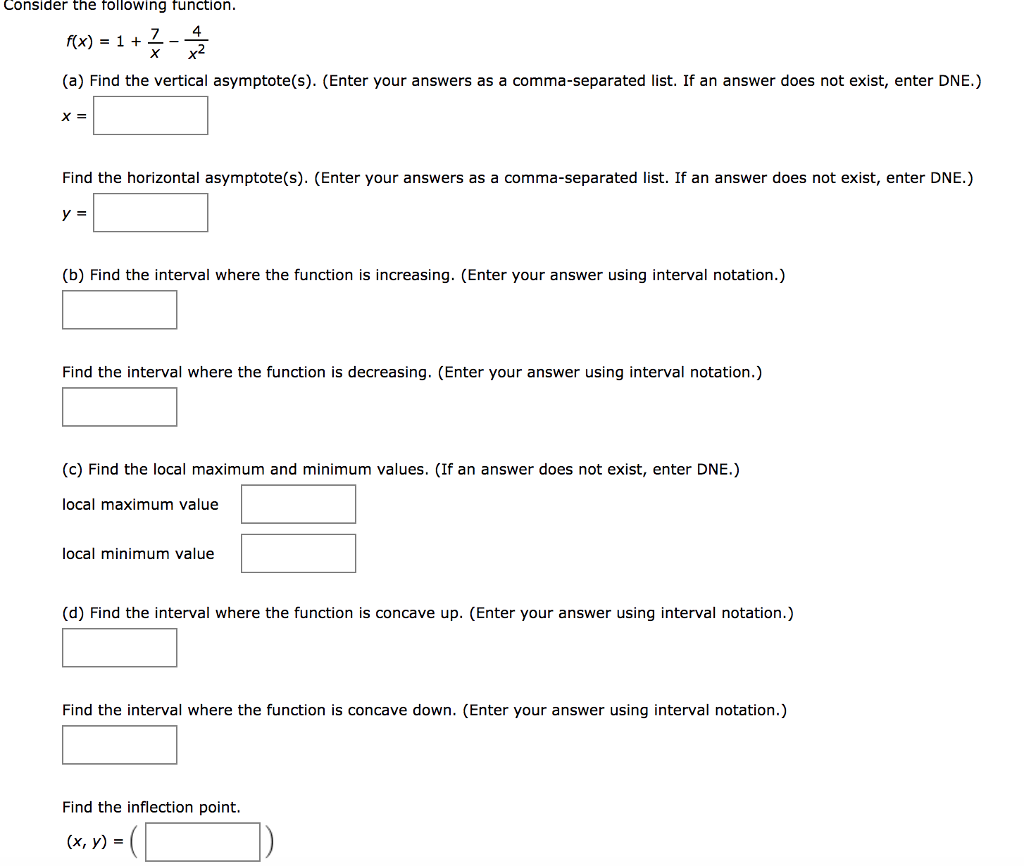



Solved Consider The Following Function F X 1 7 X Chegg Com




Using The Remainder Theorem Find The Remainder When F X Is Divided By G X And Verify The Result By Actual Division F X 4x 4 3x 3 2x 2 X 7 G X X 1
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andFunction should remain real so math√(x^2–1)/mathshould not be equal to zero so math x^2–1 \neq 0/math mathx^2=1/math Or mathx=\pm 1/math And2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all x




Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12




What Is The Equation Of The Normal Line Of F X X 3 3x 2 7x 1 At X 1 Socratic
Feb 07, 1986 · Directed by Robert Mandel With Bryan Brown, Brian Dennehy, Diane Venora, Cliff De Young A movie special effects man is hired to fake a reallife mob killing for a witness protection plan, but finds his own life in danger3 Let f and g be two differentiable real valued functions Show that any function of the form z = f(xat)g(x−at) is a solution of the wave equation ∂2z ∂t 2 = aBETTER AUDIO!ƒ(x)Chocolate Love Ver 2Credits SMEnt, LG CYONSpecial Thanks cityincolors for editingIf Reuploaded, please give credit




Functions Inverses Ppt Download
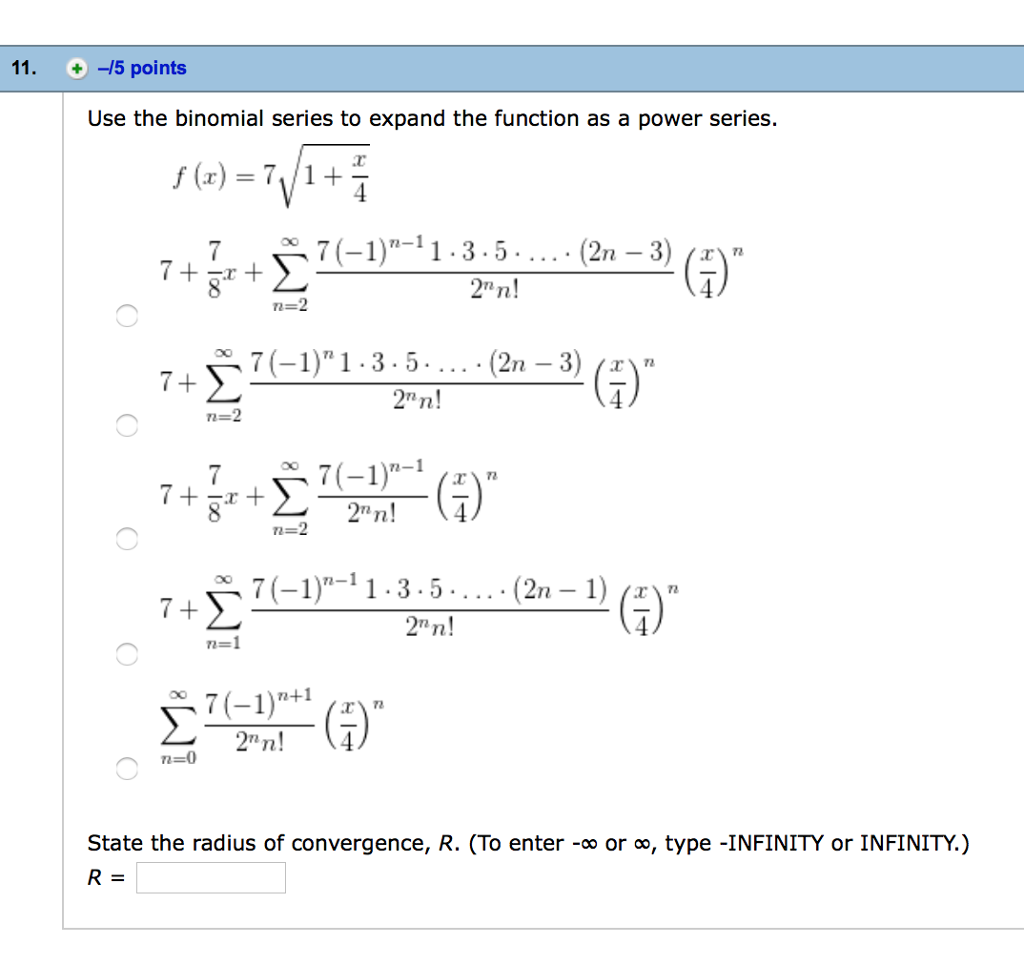



Use The Binomial Series To Expand The Function As A Chegg Com
For instance, when D is applied to the square function, x ↦ x 2, D outputs the doubling function x ↦ 2x, which we named f(x) This output function can then be evaluated to get f(1) = 2, f(2) = 4, and so on Higher derivatives Let f be a differentiable function, and let f ′ be its derivativeThen, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg( f ⋅ g ) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f ( x ) = 0 to also be undefined so that it follows the rules of a norm in a Euclidean domainThe output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressing




Newton S Method And Its Extensions Ppt Download




F X 1 7x 5 হল F X 1 ও F X 2
Mar 21, 18 · (oo, 1) uu 0, oo) Given f(x) = x^2/(1x^2) Let y = f(x) and attempt to solve for x y = f(x) = x^2/(1x^2) = (1(1x^2))/(1x^2) = 1/(1x^2)1 Add 1 to both ends to get y 1 = 1/(1x^2) Multiply both sides by (1x^2)/(y1) to get 1x^2 = 1/(y1) Add x^21/(y1) to both sides to get 11/(y1) = x^2 In order for this to have a real valued solution, we require 11/(y1) >= 0 That is yYou also asked if f(x) 2 and f(x 2) are different Yes they are The placement of the parentheses makes a difference For example with your graph above, when x = 4, f(x) = 0 and hence f(x) 2 =0 2 = 2 But f(x 2) = f(4 2) = f(2) = 2 In the second expression, since 4 2 is inside the parentheses you evaluate it first to get 22 If a < b, then F(a) ≤ F(b) for any real numbers a and b 163




Find A Power Series Representation For F X 1 7 Chegg Com




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
Engineering in your pocket Now study onthego Find useful content for your engineering study here Questions, answers, tags All in one app!




For All Real Values Of X The Minimum Value Of 1 X X 2 1 X X
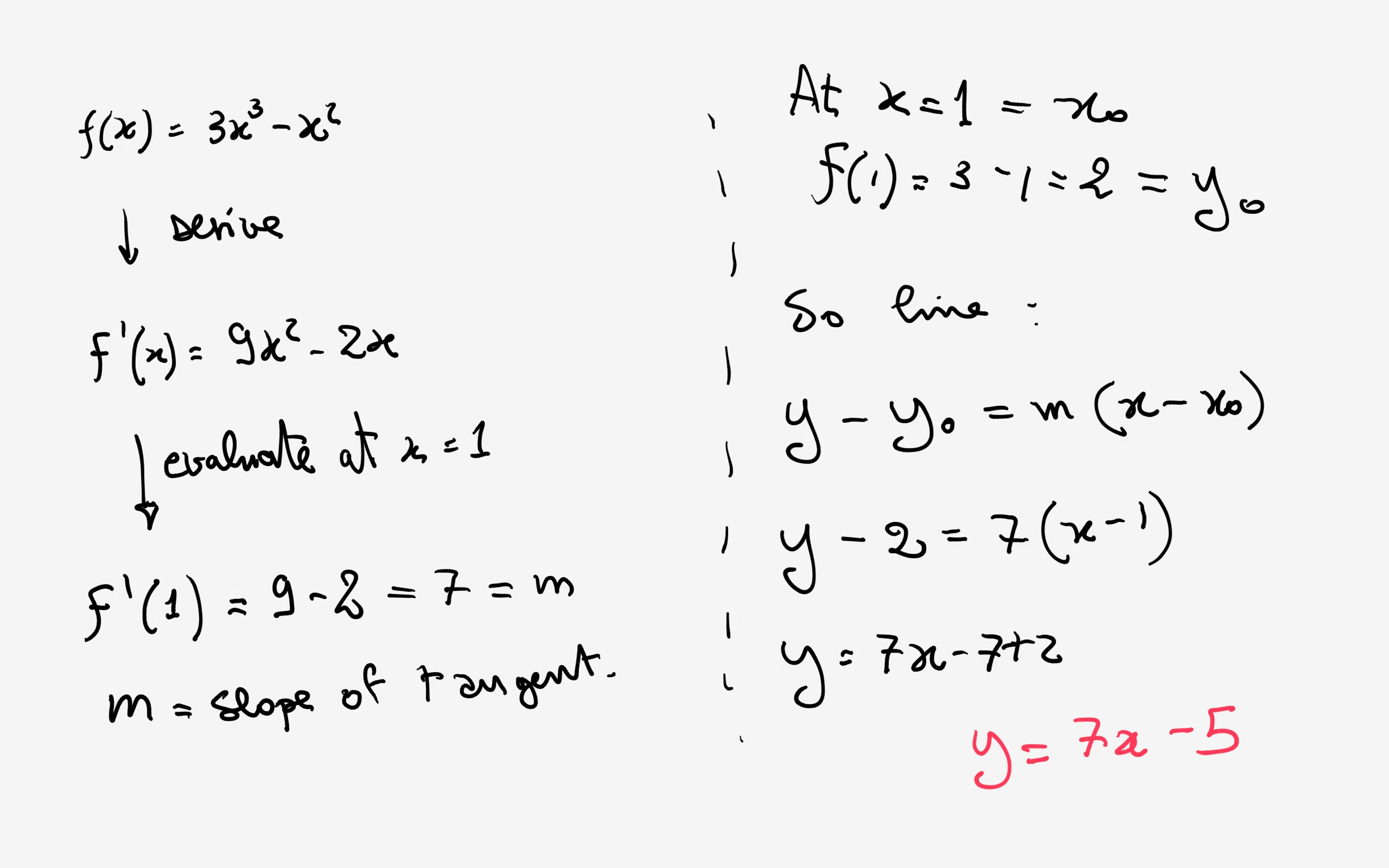



How Do You Find The Equation For The Tangent For The Curve F X 3x 3 X 2 At X 1 Socratic




The Function F X 2 1 7x Can Be Represented By Chegg Com




Calcuuuullloooo Entertainment General




Ex 6 5 2 Find Max And Min Values I F X X 2 1
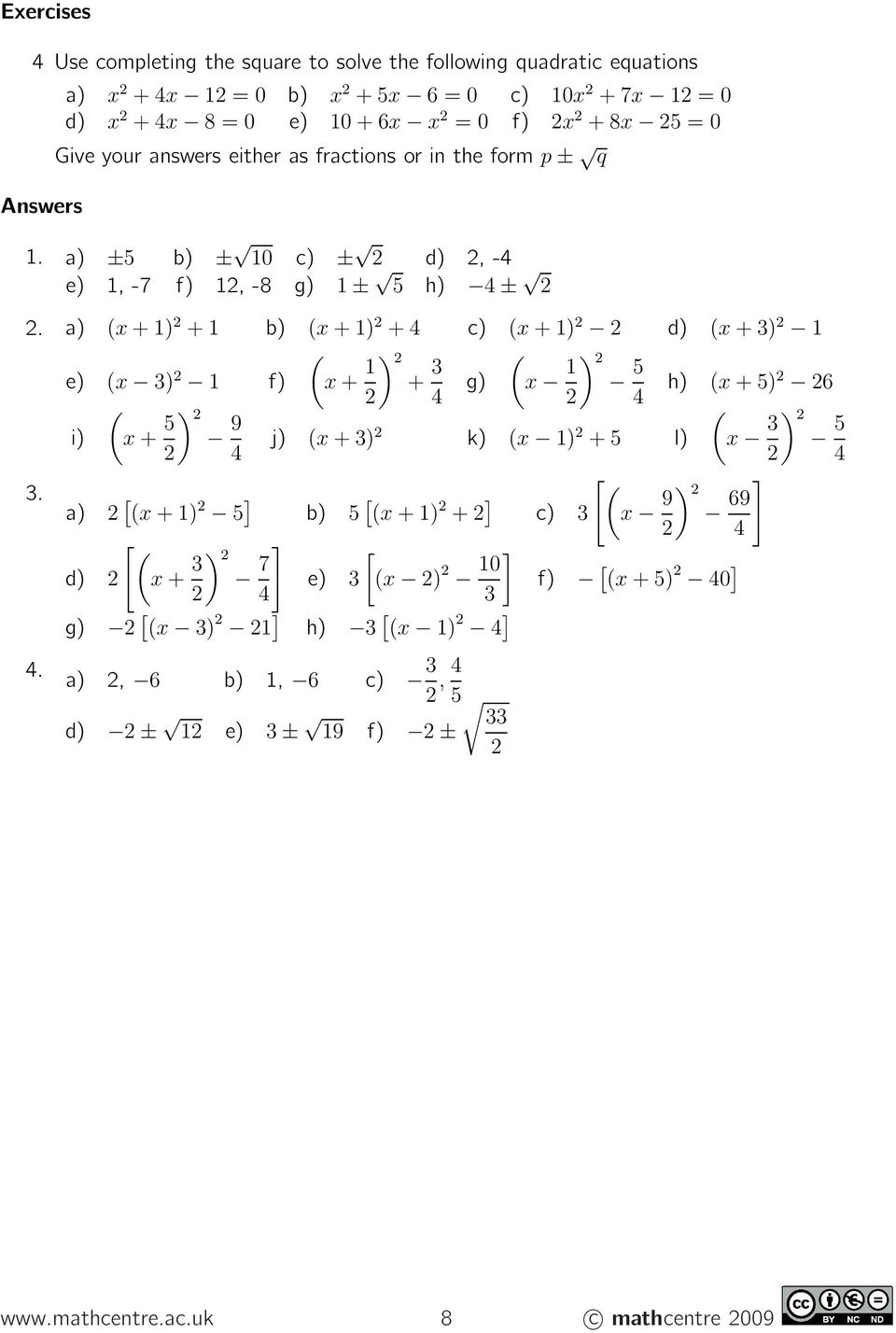



Completing The Square Pdf Free Download



Question 7 Given Function F Defined By Fx X 12x Gauthmath




Writing Exponential Functions From Tables Algebra Video Khan Academy




Rd Sharma Solutions For Class 10 Chapter 8 Quadratic Equations Exercise 8 6 Avail Pdf




Answered A Table Of Values For A Linear Function Bartleby




Solucionario Sullivan Docsity




Calameo Ecuaciones




Answered Suppose F X 4x 5 Compute Each Bartleby




अगर सम र ह F X X 3 3 1 7 X 2 3 A 2 9 X 1 एक सक र त मक ब द




Inverse Functions Ppt Download




Let F R R F X 2 X 3 2f X 2 3x 5 6x 2 10x 17 X Epsilon R Then The Value Of F 5 Is




What Is The Equation Of The Normal Line Of F X Sqrt X 1 X 2 3 At X 2 Socratic




Diketahui F X 2x 1 X 2 Nilai F 1 7 Tolong Dijawab Ya Kak Brainly Co Id




Answered Assume F G Are Differentiable Bartleby




Solved Find A Power Series Representation For F X 1 7 Chegg Com




If F R R Satisfies F X Y F X F Y For All X Y In R And




If G X Log F 2 X F X 1 F X 2 3f X 3 Sin 1




A Find A Power Series Representation For The Chegg Com




Handbuch Der Bibliothek Einstufung Und Regal Anordnung Grossen Und Preise S Nr Grosse N D Best Nr Grosse R 1 1 7 X 5 I X Li 1 0 17 2i X9 X3 Durch
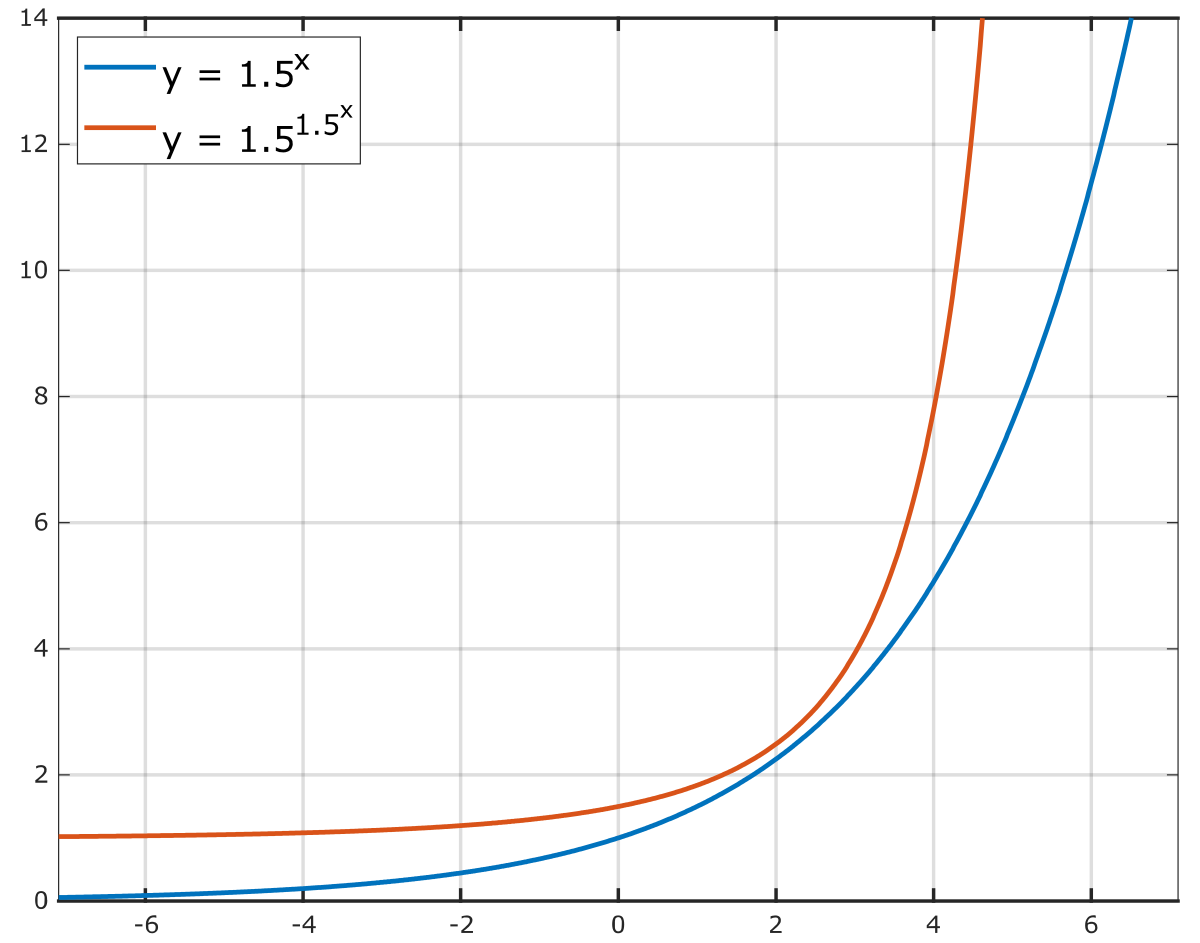



Double Exponential Function Wikipedia



Solved If F X 8x 16 Then Find F 1 X Determine If The Following Functions Are Inverses Of Each Other F X 7x 14 G X 1 7 X 2 3 Course Hero




Answered 3 2 1 1 7 5 3 1 F X 3 5 7 1 Bartleby




If F X X 2 5x 7 Evaluate F 2 F 1 1 3 Brainly In
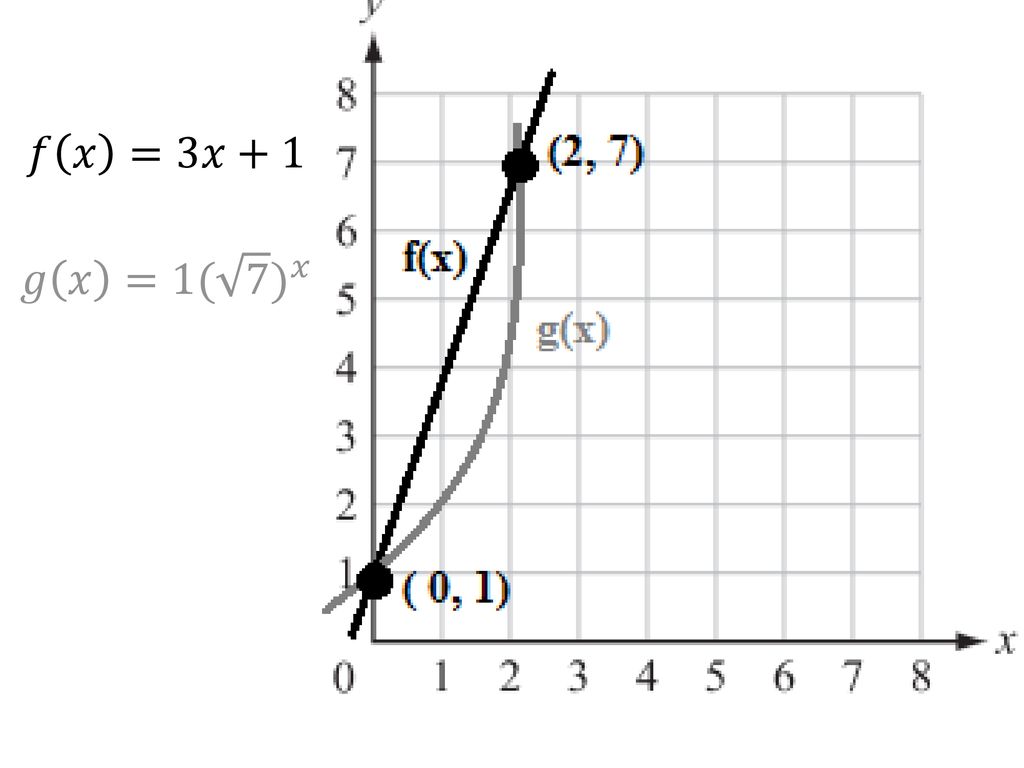



I Can See Can T You 2 7h Date 10 08 18 Ppt Download




If F R R Be Defined By F X X 2 1 Then Find F 1 17 And F 1 3




Section 2 7 One To One Functions And Their Inverses Pdf Free Download




Inverse Derivative Problems Key
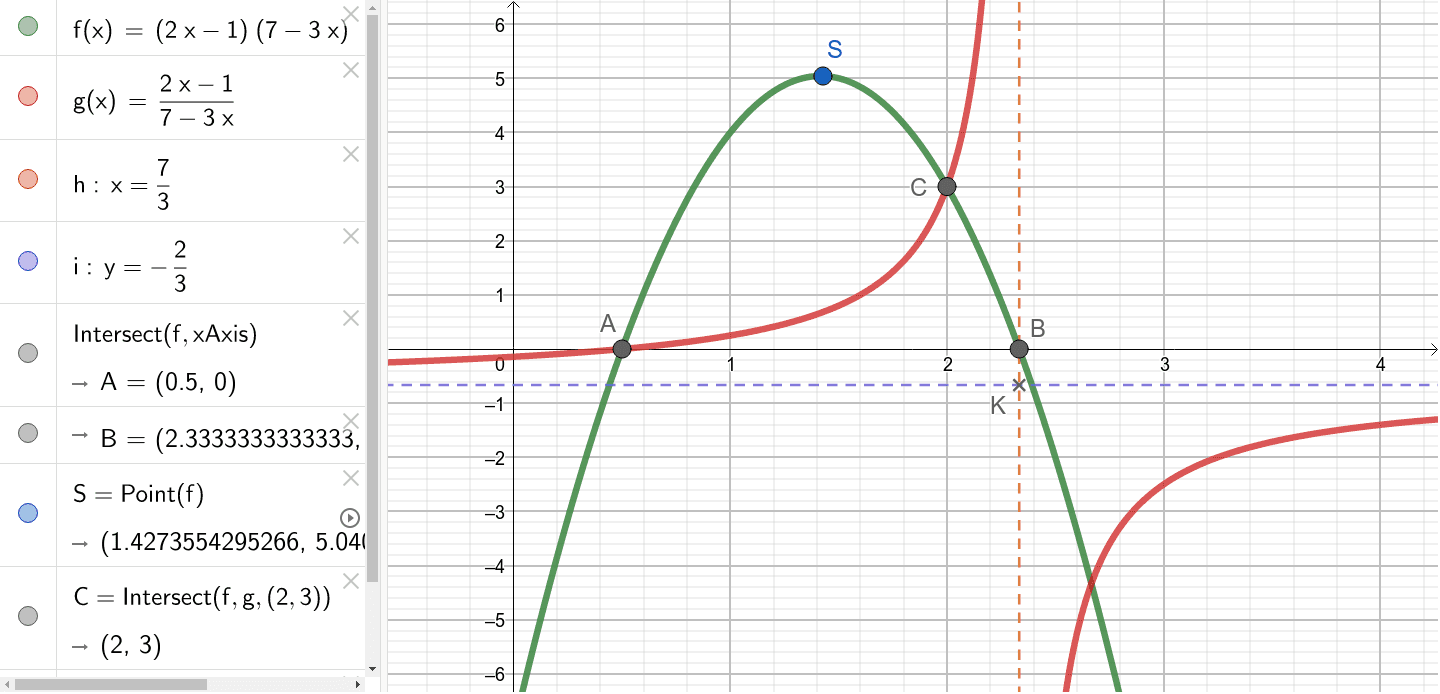



F X 2x 1 7 3x G X 2x 1 7 3x Geogebra




The Domain Of F X Sqrt X 7 X 5 Is




Ex 5 1 7 Find All Points Of Discontinuity Of F X X 3




Answered 1 7 2 6 H 4 X 12 6 G X 3 F X 9 3 1 Bartleby
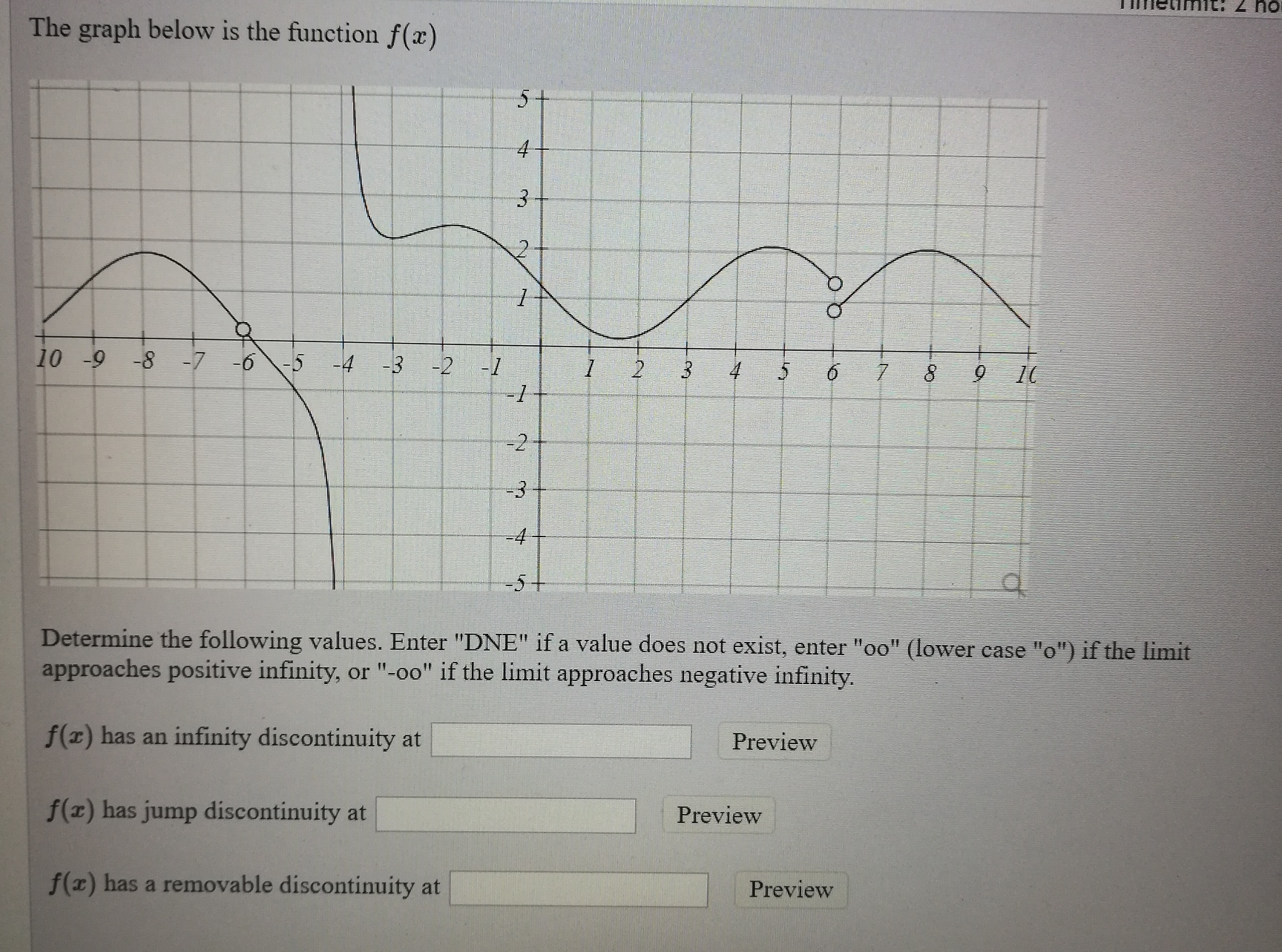



Answered The Graph Below Is The Function F X 5 Bartleby




I Basic Maths Hand Book Logarithm Algebra




If F X X 2x 7 Find X For Which F X F X 1 5 Brainly In




7 Identify Any Holes In The Graph Of F X X 7 7x Chegg Com




Ex 7 6 1 Solve A 2 3 1 7 B 3 10 7 15 C 4 9 2 7 D 5 7




Ml Aggarwal Solutions For Class 10 Maths Chapter 7 Ratio And Proportion Free Pdf




Simplify 5 1 7 2 5 2 7 4 7 2 5 2 7 3 5 3 7 5 5 2 Brainly In




Finding Linear Equations




Find The Approximate Value Of F X 2x 3 7x 2 2x 3 When X 2 002




Let F X 7 72 Compute F X 7 7x X F 1 14 Chegg Com




F X Atan 1 1 X 4 If 0 Lt X Lt 4 Btan 1 2 X 4



Solved Find The Inverse Of The Function F X 8x 16 Determine If The Following Functions Are Inverses Of Each Other F X 7x 14 G X 1 Course Hero




Rd Sharma Class 9 Solutions Maths Chapter 6 Factorization Of Polynomials




If F X X 7 And G X X 7 X In R Then D Dx Gof X




Photovoltaik Waschburste Solar Teleskop 2 1 7 3 M F Kranzle Hochdruckreiniger X Kaufen Bei Firma Joachim Gall
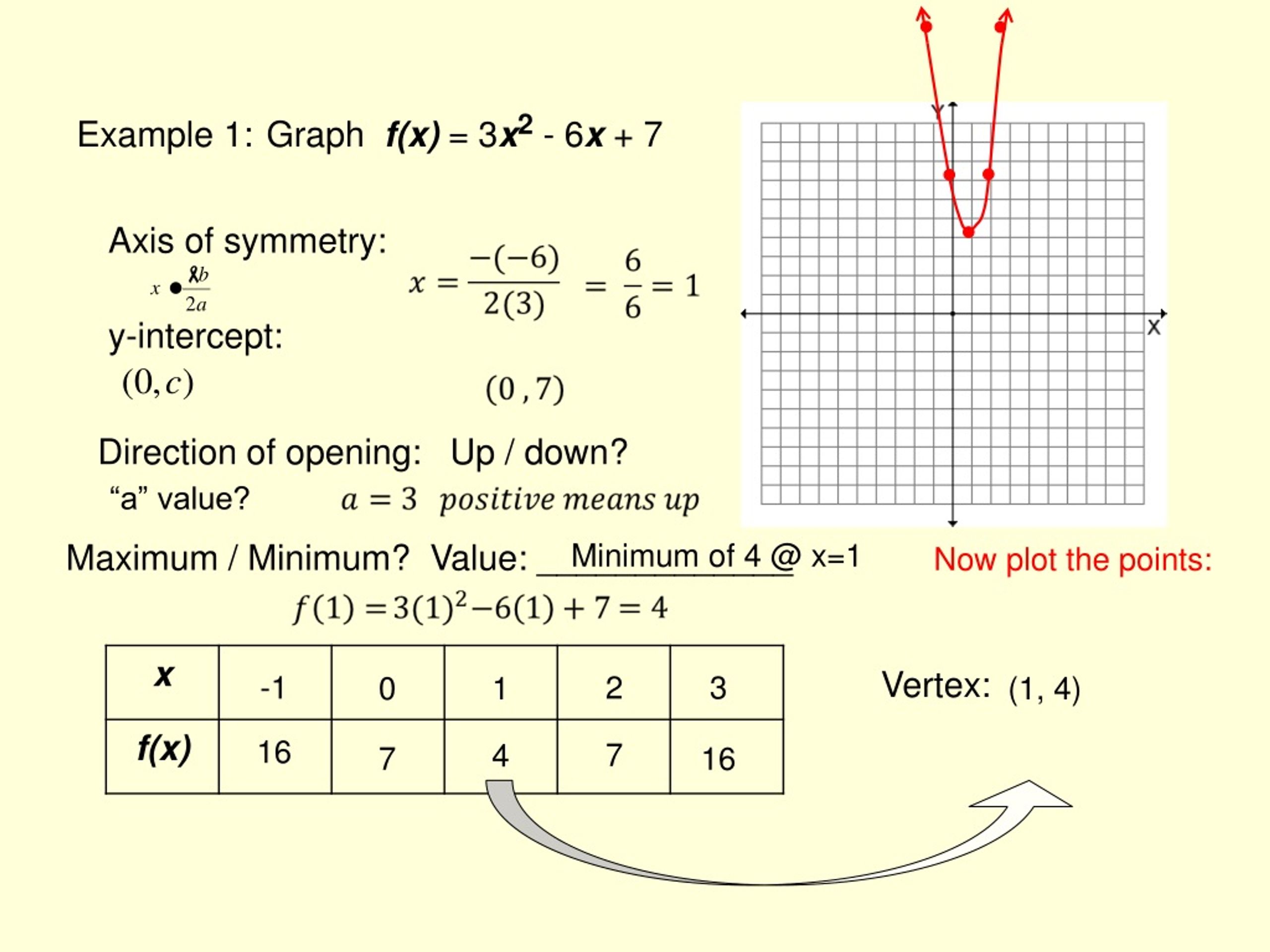



Ppt Algebra 2a Unit 2 Powerpoint Presentation Free Download Id



Use Differentiation To Find A Power Series Chegg Com




Function Notation A Function Is A Job Ppt Download




Ex 5 2 9 Prove That F X X 1 Is Not Differentiable




A First Besicovitch Ursell Knopp Functional Two Triangle Pair Function Segmentation Triangle



0 件のコメント:
コメントを投稿